When telegraphy was the mainstream of telecommunication, telegraph codes were used to replace words, phrases, or even sentences with short code groups for transmission. For organizations having a large traffic in telegraphy, carefully compiled telegraphic codes, when used by a trained clerk, provided a significant reduction of cost to justify hiring a code clerk. In this sense, any telegraphic code provided for data compression. (Even data compression today (entropy encoding) uses the same idea of making a list of frequently occurring patterns and replacing them by shorter patterns.)
In commerce, so-called figure codes were used, whereby various kinds of information such as the product, quantity, and shipping term with digits of one number, which is then converted to an alphabetical letter group for transmission. Generally, one code word could contain up to ten letters, though it may vary depending on the time and region (for details, see another article). Thus, code compilers developed various schemes to pack as much information as possible into a ten-letter code group. This may be the most developed form of data compression in the age of telegraphy.
The typical procedure was as follows.
1. Encoding Step represents various information with each digit of a number. For example, a table of 100 products numbered 00-99 is used to determine the first and second digits, a table of 100 quantities is used to determine the third and fourth digits, and a table of shipping term is used to determine the fifth digit.
2. Number Translation Step translates a number (with 10, 12, 13 digits etc.) into a ten-letter alphabetical code word.
The translation of the number encoding the various information into letters is based on two considerations. First, the international telegraph regulations treated a meaningless sequence of letters/digits as "cipher", which was to be counted as one word for every five letters. On the other hand, a "code" word could include up to ten letters, allowing more information to be packed in one telegraphic "word." Secondly, an error in one character in transmission of a number simply results in another number, having a completely different meaning, whereas code "words" may still be discernible albeit an error. Essentially, this means the alphabetic code provides more information per character and thus allows a code with high capability of error detection and error correction.
Table of Contents
Early Encoding Schemes without Numbers
Translating Figures into Letters
Figure Codes of up to Ten Digits
The idea of representing different kinds of information with digits in a number may seem straightforward with hindsight. Before this became common, however, there had been a scheme for representing several kinds of information with a code word by use of a table.
Meyer's Cotton Telegraph Code (1871)
Private Telegraphic Code (1871, New Orleans and Liverpool)
Watts's Telegraphic Cypher (1872, Liverpool)
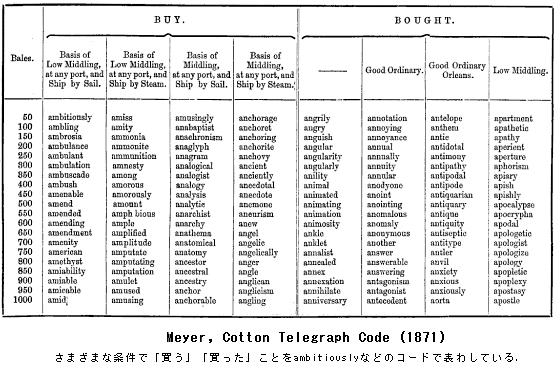
Assigning different code words for different combinations of information was tedious and there emerged schemes to represent a specific meaning with a prefix/suffix:
Electro-Magnetic Telegraph Vocabulary, or, condensing correspondent, designed to communicate commercial and other general intelligence, in abbreviated form and at small expense (1846, Baltimore) by John Wills
Parker's Combination Telegraph Code (1880) by Thomas Parker
and schemes to represent various information with syllables to make up a code "word":
Telegraph Cypher for Transmitting Telegrams relating to Foreign News, Stocks, Gold, Cotton, Financial Matters, etc., in a Commercial Form (1867) by Martin K. Thompson.
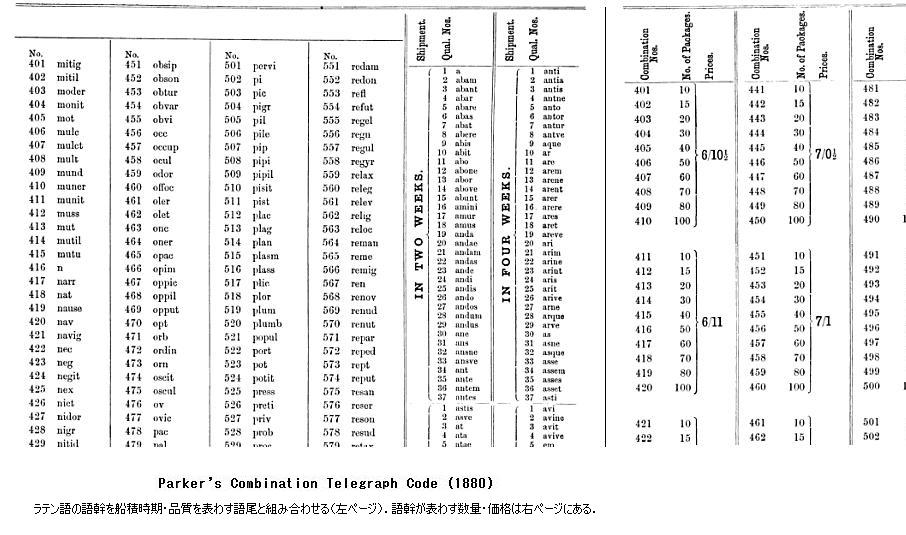
The idea of conveying information with digits in a number appears to have emerged around 1880. The two-step procedure of encoding with a number and then translating the number into letters facilitates compiling and using codes. In particular, the kind of information to be conveyed may vary depending on the user and thus the encoding tables may be designed by the user as a private code. On the other hand, code compilers may create a codebooks specially designed only for figure translation.
As one early example of conveying information with digits of a number, The Telegram Code (1880, 3rd. ed.) by Ager describes on p.iv that the five-figure groups accompanying every code word allow transmitting in one word quantities, prices, and qualities, or other particulars of an offer, order, contract, purchase, sale, &c.
According to the example given, the code word "Mutual" (representing "We recommend purchase of -- as crop is injured") is accompanied by the number "29795", which may be used to mean "within 21 days" (2), "to Glasgow" (9), "at 16s. 9d. per barrel" (79), and "this is order number 5" (5). Blank tables are provided for the user.
Another codebook by Ager (probably referring to Ager's Standard Telegram Code of 100,000 Words (1879) and its supplements) is described in a book in Japanese: Ueda Kotaro, Gaikoku Kawase to Denshin-Ango (1895). According to the scheme, the first two digits of a five-figure number represent the product and the latter three digits represent combinations of quantity, shipment, and price. The quantity, shipment, and price are represented by numbers 1-5, 1-5, and 1-25 according to tables, respectively, and the three numbers are translated into a three-figure number according to a combination table, of which the ordinate represents 5*5=25 combinations of quantity and shipment and abscissa represents 25 prices, resulting in 625 combinations and associated numbers. (The tables are on p.41-47 in Ueda (1895).)
Naively, three kinds of information might have taken one digit for 5 quantities, another digit for shipment, and two digits for 25 prices, totalling four digits. But use of four tables allows 5*5*25=625 combinations to be encoded in three digits.
The five-figure number encoding such trading information is translated into a code word with a table listing "00000 aafsch", "00001 aakste", "00002 aalbes", ..., "00252 Abbaruffo", ..., "99999 Iravail."
The above scheme requires a table for translating figures into letters. Many codebooks had serial numbers assigned to code words. Possibility of representing figures with code words accompanied by those serial numbers was known from the earliest period of telegraphic codes (see another article). The technique for encoding various information with figures took advantage of the association of numbers and code words in existing codebooks, without regard to the words/phrases represented by those code words. Such use of existing codebooks is described in, e.g., Macgregor's Variation Tables for Code Telegraphing (1881).
There appeared codebooks specialized for translating figures into code words, including a series of codebooks by Whitelaw.
In the 1880s, there appeared codebooks such as "Exchange" Code and "Nonpareil" Code for translating five-figure numbers into code words (another article).
Association between numbers and code words may be attained by simply listing English code words as in 25,000 English Words (1879) or by using combinations of Latin stems and suffixes as in Latin Combination Telegraph Code of 10,000 Cypher Words (1908).
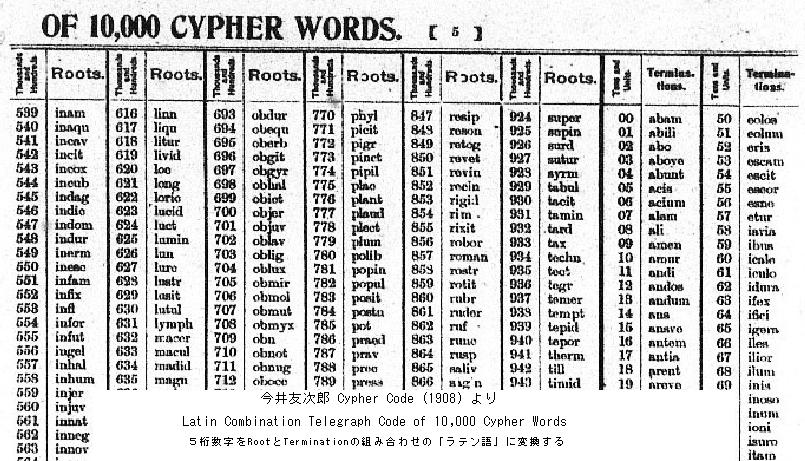
As long as real words are used, even with stem-suffix combinations, essentially, exhaustive listing of words is required. On the other hand, if numbers are translated into letters by predetermined rules, one small table may suffice.
The Westinghouse Code (1902) provides rules for translating a ten-figure number into a ten-letter "word." Specifically, the following table is used to convert every two digits 00-99 into two letters consisting of a vowel and a consonant.

It should be noted that the international telegraph regulations at the time stipulated that code words must be real words in one of the eight designated languages such as English, French, etc. Thus, Westinghouse proposes transposing the consonant and vowel as appropriate and/or using alternative letters (found in the column to the right) such that the result looks like a real word.
The 1903 revision of the international telegraph regulations (which took effect in 1904) removed the restriction that code words had to be real words, requiring only that they be pronounceable. This officially allowed systematic creation of code "words". (Soon, it became common to use artificially created five-letter code words, two of which may be concatenated to be sent as one ten-letter code word to reduce the telegraph cost by half. See another article for details.)
The China Inland Mission Private Telegraph Code (1907) also provides a table to combine two code words into a ten-letter group. It is called the G.Y.X. Table because the consonants are arranged G, Y, X, V, R, ....

Two similar code condensers of Junzaburo Yamada, who supported Sun Yat-sen, are presented in another article.
Now that the code groups did not need to be "real words", the C.I.M. Code proposed to use vowel-consonant pairs (as opposed to consonant-vowel) to represent code numbers of Chinese characters. Since each Chinese character was assigned a four-digit number (another article), an eight-letter code word could represent two characters and two ten-letter code word could represent five characters.
A similar conversion table as Westinghouse's that convert every two digits into a consonant-vowel pair is also described in Nakagawa (1916), p.733, though no trouble is taken to make the combination look more like real words. Since the consonant-vowel transposition for plausibility as a real word is no longer necessary, it is proposed to use the transposition (i.e., whether consonant+vowel or vowel+consonant) for error checking (Nakagawa, Acme). This is similar to the ideas of information embedding or digital watermarking in modern times.
The above table of Westinghouse is termed "Code Condenser". It was designed to "condense" two code words into one word via use of numbers to reduce the telegraph cost by half. To one familiar with five-letter code words in later years, concatenation of two code words into one ten-letter code word may seem trivial. However, since code words at the time were "words" with no fixed length such as Kabache, Kabakos, ..., condensing them into one word required this special procedure. Specifically, since each code word is accompanied by a five-figure number, a ten-figure number consisting of two of them may be converted to a ten-letter code word with the Code Condenser.
The Cosmos Code Condenser and American Condenser are also such code condensers. Probably so is Pieron's Code Condenser, 50% Economy without changing Codes (which the present author has not seen).
Seemingly similar titles are found on the web:
Premier Code Condenser (1907) by William H. Hawke
"Two-in-one" code condenser : a standard system for rapidly coding two code phrases in one word with perfect safety... : for use with general or private codes in English, French, German, Dutch, Spanish, Portuguese, Italian, or other language : indispensable to bankers... &c. (1910)
Composite code condenser. 12 figures in 10 letters or 11 figures in 9 letters (1919) by William George Gerlach
The Wallaby Code Condenser (1921, Melbourne) by W. E. Rockingham
(Google) A code condenser for representing two code words in a ten-letter code word by translating 6-figure numbers (0-199999) into 5-letter code words by means of rotating wheels was patented in the United States. The 5th to 6th figures are translated into two letters, the 3rd to 4th figures again into two letters, and the 1st to 2nd figures (00-19) into one letter by means of three rotating wheels, respectively.
The author Hanso Tarao is the same person as Alfred H. Tarao, who published a 13-figure code in 1913 (see below).
Notwithstanding the title referring to "14 figure", the upper seven figures and the lower seven figures must each be at most 1249999. For example, 14-figure numbers with the lower seven figures of 1250000 or greater cannot be handled. This is a "code condenser" designed to represent with one ten-letter word two code words with a number less than 1250000 from any codebook. There had been many precedents for such a "condenser" for handling numbers up to ten figures, including Bentley's 900 Million Edition (which could handle numbers up to 2999929999).
The name "Acme" reminds one of the famous codebook by A. C. Meisenbach (1923) but it had also been used in M'Kay's 'Acme' Stock Exchange Signal Code in as early as 1886.
Basically, this Acme translates the upper four figures 0000-1249 into two letters and the lower three figures 000-999 into two letters. Since tables only provide letters for numbers 000-249, the upper four figures and the lower three figures are divided by 250 and only the remainder 000-249 is encoded with two letters. This means the two letters represent the upper four figures minus either 000, 250, 500, 750, or 1000 or the lower three figures minus either 000, 250, 500, or 750. The combinations of subtrahends (there are 5*4=20 of them) are represented by one letter (which would be the third letter in the final five-letter code word), called an index.
When decoding, the first two letters and the last two letters of a five-letter code word are used to recover numbers 000-1249 and 000-1249, which are to be augmented by numbers determined by the index (the third letter).
The author says this work is characterized by (1) use of J and Y as vowels, (2) use of the index, (3) absolute secrecy provided through change of index assignment, and (4) representation of 14 figure numbers.
This authoer is the same person as Hanso Tarao above.
While the title refers to "13 Figure Code", this is to represent two code words numbered up to 280000 from any codebook in one ten-letter code word by converting numbers up to 279999279999 into ten letters. (The first half and the latter half should each be up to 279999.) The author claims that the "index" used in the condensing is his invention.
First, the 12-figure number is divided into the first half and the latter half, each consisting of six digits. Each six-digit number is divided into the first four digits and the last two digits. The first four digits are translated into two letters by Table A and the last two digits are translated into two letters by Table B. Here, the first four digits are taken modulo 700 (that is, only the remainder 000-699 after subtracting multiples of 700 is used). In this way, the first half gives the first and second pairs and the latter half give the fourth and fifth pairs of letters. The discarded multiples of 700 (i.e., either 000, 700, 1400, or 2100) for the first half and the latter half, as well as a check digit (the unit place of the sum of all the digits), are taken together to look up Table C to determine the third pair of letters.
Code compiler's response to the new revision that took effect in 1904 was quick. In this very year, several codebooks (called "code vocabulary of cipher words" or simply "ciphers") adapted for translation of numbers into letters appeared.
Whitelaw's Telegraph Cyphers, Pentasyllabic words representing two series of 10-figure groups from 0,000,000,000 to 9,999,999,999 [1904] probably translate a ten-figure number into five syllables each consisting of a consonant and a vowel, thus a ten-letter word, as in Westinghouse above.
The year 1904 also saw publication of the following
7 figures: The Economical Telegram Code Vocabulary of 10,000,000 inconvertible cipher words, each of ten letters, numbered consecutively from 0000000 to 9999999. With terminational order (Bombay)
8 figures: Beith's 10-Letter Combinations (8 Figures) (Manchester),
9 figures: McNicol's Nine Figure Code, or 1,100 Millions Pronounceable Words (Manchester).
Judging from the titles, these are similar to Whitelaw's.
The "private code" or "private commercial telegraphic code" as used by Ueta corresponds to an encoding table as used herein. The information encoded in a number is translated into a code word with a "10 figure table", though the title suggests any 10 or 12-figure code could be used.
The table includes two columns for translating a number 00-99 into two sets of two letters. First, the ten-figure number is divided into five pairs of figures. The sum of the ten figures is looked up in a separate "Control or Check Table" to determine five letters (e.g., ABBAA). Each of these five letters indicate the column to be used in translating the pair of figures into two letters.
Mosse Condenser, appendix to Rudolf-Mosse Code (1922) translates ten-figure number into a ten-letter code word.
First, the ten-figure number is divided into five pairs of figures. The five sums of the two figures of the five pairs are used to determine five letters (e.g., BBBAA) from the control table. Each of these five letters indicate the column to be used in translating the pair of figures into two letters.
This is an appendix to Acme Commodity and Phrase Code (1923). As with Westinghouse, it translates every two digits into two letters.
This is an appendix to "1926 Supplement" to K. Kagawa & Co's Special Code (1926). As with Westinghouse, it translates every two digits into two letters (there are only five vowels: A, E, I, O, U). It is followed by "3 Figure Phrase Combination Table" for encoding various information with three-figure numbers.
It is more or less straightforward to represent a ten-figure number with a ten-letter code word. However, there were figure codes that could handle numbers with twelve or more figures. Such figure codes typically use tables with multiple sections, with part of the information being conveyed by "which section is used in encoding."
This essentially converts a six-figure number into a five-letter code word by translating the first three digits into two letters and the latter three digits into three letters.
The first and second digits 00-99 are translated into two letters by reference to the column to the left. The third and fourth digits 00-99 and the fifth and sixth digits 00-99 are used as indexes to rows and columns, respectively, of a table spanning over several pages to determine a three-letter pattern.
This converts the first two digits of a six-figure number into a two-letter "prefix" and the latter four digits into a three-letter "root." By repetition of the same table sections in pages, one half word (i.e., five-letter sequence) may be found with reference to only a single page.
The upper section of a page repeats a table for associating 00-99 with a two-letter prefix, the section below which is a table for translating the remaining four digits into a three-letter root. In operation, it would be convenient first to look at the first two digits for the root (the third and fourth digits of the six-figure number). About the middle of the page, in the top part of the root table, there are printed 00, 01, 02, 03, ..., which may be used to open to the page containing the relevant block. Then, the prefix table above that block is used to determine the two letters for the first and second digits of the six-figure number. Since each block is divided into four columns, in using the root table, the same column as that in which the prefix was found in the block is used to determine the letters corresponding to the last four digits.
For example, when 750104 is converted to a code word, first, the block containing the third and fourth digits ("01") is found (p.1) and the two-letter pair corresponding to "75" is found in the prefix section. In this upper section of the page, a table including 00-99 (of which there are two alternate versions) is repetitively printed. For "75", the two-letter pair "af" or "ak" is found depending on the block. For the block "01", it is "ak." In the block "01", one looks down the column in which 75=ak has been found and finds 04=ape in the root table (which associate three-letter patterns to 00-99).
Catalogs such as WorldCat also lists Kendall's 12 figure Cypher Code. In strict accordance with the requirements of the London Conference of June-July, 1903, etc. (Lieber Code Co., New York, London, 1908, 35pp.), which may be the same as above; and The "Cheepandi" 12 Figure Cypher Code (1909, New York). There is also Eureka Cipher Code, 13 figures (1919, New York, 69pp.) (found in Catalog of Copyright Entries) appears to be an augmented version of the above.
Another Kendall (Oliver S. Kendall) is given as the author of The "International" 12 Figure Cipher Code, Being Composed of a Million Million Artificial Words as Sanctioned by the Telegraphic Conference Held at Lisbon, 1909, Together with a Special Check System for the Correction of Mutilations (1910, 35pp.). Of the many codes attributed to this author, a 14-figure code will be described below.
The title page bears an imprint of "Lieber Code Co., New York-London" but the bibliographic information at the back of the volume says the publisher is Japan Gazette Shimbun-sha (in Yokohama). The bibliographic information gives Kendall's address in Yokohama but his contact on the title page is a post-office box in Kobe.
This is essentially a 12-figure code based on translation of 6-figure numbers into 5-letter code words. The "13-figure code" is achieved by providing just two sets of such conversion tables, with Part I for 13-figure numbers beginning with "0" and Part II for ones beginning with "1". So, for those users who do not need a 13-figure code, a volume including only "Part I" was separately sold at half the price.
Essentially, a 6-figure number is translated into a 5-letter code word by means of a table (divided onto multiple pages) indexed by the 1st and 2nd figures 00-99 on the sides and the 3rd and 4th figures 00-99 on the top to find corresponding three letters and tables indexed by the 5th and 6th figures to find two letters. In Part I (the first figure of the 13-figure number is "0"), the same tables are used both for the prefix (corresponding to the first 6 figures) and suffix (corresponding to the latter 6 figures). In Part II (the first figure is "1"), separate sets of tables are provided for the prefix and suffix.
The title page advertises that this "will telegraph TWO WORDS from any 5 or 6 figure code in ONE WORD, and give check figures." That is, this was intended as a code condenser.
The author gives an example of using the first two figures of a 13-figure number as an indicator to specify the codebook(s), the 3rd to 7th figures and 8th to 12th figures as referring to two code words in the specified codebook(s), and the 13th figure as a check. The suggested indicators are: 00 (the following ten figures should be interpreted as 5-figure numbers in Western Union or ABC), 01 (6-figure numbers in Western Union or ABC, with the leading "1" omitted), 02 (5-figure number and 6-figure number in Western Union or ABC), 03 (6-figure number and 5-figure number in Western Union or ABC), 04 (Liebers or A1), 05 (Liebers or A1 and Western Union or ABC), 06 (Liebers or A1 and 6-figure numbers in Western Union or ABC).
The author says the letters found in the tables are selected such that letters likely to be mutilated (ab:00 vs. ad:50) have "a wide difference in number."
Essentially, this translates the first three digits of a six-figure number to two letters and the latter three digits into three letters, resulting in a five-letter code word. The first three digits are looked up in the Upper Table of the pages to find the two letters. The Lower Table on the same page is used to find the three letters for the last three digits.
Probably (I have not seen its copy), the Upper Table gives two letters for numbers 000-999 in 10 pages. Since two-letter combinations provide only 676 patterns, some combinations should occur more than once. The Lower Table must have provided 000-999 on each page but the same three-letter pattern must have never occurred throughout the pages, which ensures that the resulting five-letter group is unique to each six-figure number.
When decoding, the last three letters of the five-letter code word (half word) is looked up in the Lower Table to find out the relevant page. Then, the last three figures are found in the Lower Table and the first three figures are found in the Upper Table by using the first two letters as a key.
Google gives a fuller title The Ideal Code Condenser: Being a Thirteen Figure Code (0,000,000,000,000 to 9,999,999,999,999) for the Purpose of Enabling a Number of Different Numbered Codes to be Employed in the Same Message at the Rate of Two Phrases to One Code Word, the Recipient Being at the Same Time Informed from which Code to Read Each Part of the Message, with Two-figure Safety Check Against Mutilations. With Full Instructions in English, French and German. A review of the second addition appeared in the 18 November 1913 issue of The Dominion: "The object of a Condenser is by means of the figures to 'condense' two code words taken from a numbered code such as the A.B.C. into one artificial word, thus saving half the cost of transmission. It is claimed that te 'Ideal Code Condenser' however goes further than any other condenser on the market, as it permits of several different numbered codes being employed in the same message at the rate of two phrases to one word, the recipient being at the same time informed from which code to read each part of the message."
This can translate 13-figure numbers from 000 00000 00000 to 499 99999 99999 into ten-letter code words. (When 12-figure numbers and 13-figure numbers are mixed, the first digit 0, 1, 2, 3, 4 of the 13-figure number should be replaced by "none", 0, 1, 2, 3, respectively.) Five tables ("Section" A-E), each for translating 00-99 into two letters, are provided. The first digit is used in consulting Table I to determine the section to use for translating the second and third digits into two letters. Similarly, the fourth digit is used in consulting Table II to determine the sections to use for translating the fifth and sixth digits and the seventh and eighth digits into two letters and the ninth digit is used in consulting Table II to determine the sections to use for translating the tenth and eleventh digits and the twelfth and thirteenth digits into two letters.
In order to satisfy the pronounceability requirement, Section A provides a vowel+consonant pattern and Section B provides a consonant+vowel pattern. Since the second and third letters and the tenth and eleventh letters are either A or B, the resultant ten-letter code word includes at least two vowels. But the consonant+consonant pattern in Sections C, D, and E may result in hardly pronounceable patterns. (In the following, such an example has been chosen.)
This is an appendix to Acme Commodity and Phrase Code (1923). It translates a 13-figure number (12 digits + check digit) into ten letters but the first three digits must be up to 129. First, the first three digit is used to determine a five-figure pattern, each digit (1-4) of the five-figure pattern indicates the table to be used in translation of the subsequent ten figures, i.e., five pairs of figures. Each table is for translating 00-99 into two letters. The first table provides consonant+vowel, the second table provides vowel+consonant, the third table provides consonant(B-M)+consonant (N-Z), the fourth table provides consonant (N-Z)+consonant (B-M). Thus, the recipient would know which table should be used to decode the letters of each pair in the code word into figures.
For the first three digits, if combinations of 1-4 are fully exploited, the number of possible combinations amounts to 45=1024, which may seem to imply there is no need for the restriction of the first three letters to 129. Since the international telegraph regulations stipulated that code words must be pronounceable, it appears care was taken such that "3" and "4", which represent consonant+consonant combinations, should not follow one another or should not appear at the beginning and that sequences such as "241" and "231" are avoided because they result in succession of four consonants. (Absence of Q may also be for the pronounceability.) Even when such care was taken, 126 provides "24212", which leads to a bizarre "word" such as "udxbubcuah". However, at this time, the requirement of "pronounceability" was applied rather sparingly and presence of some vowels might be sufficient for admission.
Nakagawa Shizuka (1916), Shinsho Seikan (Digital Library from the Meiji Era) around p.735 gives the following as figure translation tables for 12 figures or more, which were used in Kobe at the time.
Kendall's 12 Figure Cypher Code
Voller's 12 Figure System
Non Plus Ultra Cypher Code (12 Figures)
Kerr's 13 Figures Code
Schofield's 13 Figure Condenser
Yamada's 13 Figure Cypher Code
However, Nakagawa remarks that since 13-figure codes do not allow arbitrary values up to 9 for the first digit and often result in unpronounceable code words, they were not widely used as of 1916.
The US Catalogue of Copyright Entries (Google) for the year 1916 registers Schofield's 13-Figure Telegraph Code (2nd ed., 2 sheets).
This is a three-letter code, of which three code words plus one check letter forms one ten-letter code word for transmission. The second edition proposes that this may be used as a 13-figure code. Since each code word is accompanied by a four-digit number, it could be used for translating each of the three four-digit numbers derived from the 12-figure number into a three-letter code word. (The thirteenth figure is for checking.)
In the 1930s, the "pronounceability" requirement was relaxed and any sequence of three-letter code words could be used.
The "pronounceability" requirement, which restricted the code word patterns for more than twenty years, was relaxed in the 1928 revision of the international telegraph regulations and was abandoned in the next revision, which took effect in 1934. This opened a way for number translation for 14-figure numbers.
Since five letters (the number of whose combinations amounts to 265=about 107) allow representation of up to 7-figure numbers, ten letters provides representation of up to 14 figures.
Rather surprisingly, "14-figure code" was published as early as 1906. From the word "Condenser" in the title, it was probably intended for representing two or three code words (which were real words or words that look real, typically longer than five letters) with ten letters via a 14-figure number.
This treats the 7th and 14th digits in a special way. It is provided that either the 7th and 14th digits or only the 14th digit is used for check. In the latter case, the sum of the first thirteen digits (except for the 7th) modulo 5 is used as a check digit.
This appears to be more or less like the Mosse Condenser above. The 1st and 2nd digits determine the columns used for the 3rd and 4th digits, the 5th and 6th digits, and the 8th and 9th digits. The 7th and 14th digits determine the columns used for the 10th and 11th digits and the 12th and 13th digits. The information of the 1st and 2nd digits and the 7th and 14th digits is preserved in the form of "which table was used."
The author Albertus Charles Meisenbach published a 13-figure code as an appendix to Acme Commodity and Phrase Code (1923) as described above. It appears he immediately took advantage of the 1928 revision of the regulations to publish a 14-figure code. In 1937, what seems to be its revision was published.
This ten-page booklet claims to be compliant with the 1928 revision of the international telegraph regulations. This translates a 14-figure number after dividing it into the first four digits (which must be up to 1499) and the latter ten digits. (The last two digits should be the sum (or the last two digits thereof) of the numbers represented by four pairs of the 5th to 12th digits, providing a check sum.)
First, the Indicator Table (similar to the control table of the Mosse Condenser) is used to determine an indicator (a five-figure number 11111-65122) corresponding to the first four digits 0000-1499. Each digits of the indicator ranges form 1 to 6 and indicates which column of the Coding Table 1-6 should be consulted. Specifically, each digit of the indicator indicates the column of the Coding Table for each of the pairs of the last ten digits. Each column of the Coding Table is for translating a pair of figures into two letters. (The ten-letters transmitted correspond to the latter ten figures and the information about the first four digits is encoded in "which table was used.")
In the Coding Table, column 1 provides vowel+consonant and column 2 provides consonant+vowel. By ensuring that the five-figure number of the Indicator Table includes three or more "1" or "2", it can be ensured that the resultant ten-letter code word includes at least three vowels, thus satisfying the conditions of Category A of the 1928 revision of the regulations.
Another number translation table by Imoto is described here (albeit being not "13-figure"). Again, this claims to be compliant with the 1928 revision of the international telegraph regulations. This translates an 8-figure number (up to 1799999 + a check digit) after dividing it into the first three digits and the latter four digits (+ the check digit).
First, the Indicator Table is used to determine an indicator (a three-figure number 111-665) corresponding to the first three digits 000-179. Each digit of the indicator ranges form 1 to 6 and indicates which column of the Coding Table 1-6 should be consulted. Specifically, each digit of the indicator indicates the column of the Coding Table for each of the pairs of the latter four digits and the check digit (the 8th digit). Each column of the Coding Table is for translating a pair of figures into two letters.
This claims to be compliant with the international telegraph regulations which took effect in 1934. This can translate any 7-figure number or 8-figure numbers up to 11,419,999 into a five-letter code word.
The 7-figure case is first described. First, the section marked with a number in red matching the first two figures is found. The section lists "Key" and "Odd & Even Mark" for the remaining 5 digits. The column "Odd & Even Marks" is used to find the odd (-)/even (=) pattern of the five digits (there are 25=32 such patterns), which is accompanied by a 5-figure "Key". Then, each digit ("Figure") (0-10) of the original 5-figure number is used with "Key" (1-5) to refer to a Coding Table to determine the corresponding letter. (There are only 25 letters of the alphabet (X is not used) for the 10*5=50 combinations. So the same letter is assigned for the original digit 1 and 2, 3 and 4, and so on.) Thus, a 5-figure number is translated into a 5-letter code word.
When decoding, each of the five letters provides the corresponding original digit (of which two candidates, odd and even, are given in the table) and a Key digit. When the 5-figure Key is identified for the five letters, the corresponding entry is found in the column of Key, which is accompanied by an odd-even pattern, which in turn uniquely decides each digit from the two candidates. From the number in red associated with the section to which the entry belongs, the first two digits of the original 7-figure number can be known.
In the above description, the number printed in red corresponds to the first two digits but there are also 3-figure numbers in red. If the first three digits match one of these, the odd-even pattern has only four places (there are 24=16 such patterns). And the Key has "x" in its second place. The four digits are translated into a letter as described above, with the letter "X" in the second place left as it is.
Even the first four digits may match a number in red. It is used when translating an 8-figure number into a 5-letter code word. In such a case, the remaining four digits are translated into a 5-letter code word including "X", as above.
This translates a 7-figure number (of which the 7th digit is a check digit corresponding to the unit's place of the sum of the first six digits) into a five-letter code word.
1. The number is divided into the 1st/2nd digits, the 3rd/4th digits, the 5th/6th digits, and the 7th digit.
2. The 1st/2nd digits, the 3rd/4th digits, and the 5th/6th digits are used to consult a table consisting of four columns marked with graphical symbols % (00-24), o (25-49), @ (50-74), and # (75-99), which indicate a letter for the respective two digits 00-99. This results in three letters and three symbols called a symbol sequence (%%%, %%o, ..., ###). (The symbols %, o, @, and # used herein are substitute characters for four graphic symbols: a triangle, a circle, a double circle, and a square.)
3. There is another table of which the rows correspond to the symbol sequences (%%%, %%o, ..., ###) and the columns correspond to 0-9 of the 7th digit. This gives two letters for the 7th digit.
4. The three letters from Step 2 and the two letters from Step 3 yield a five-letter code word.
For decoding, the five-letter code word is divided into the 1st to 3rd letters and the 4th and 5th letters.
1. The 4th and 5th letters give the 7th digit and the symbol sequence (%%%, %%o, ..., ###).
2. The symbol (%, o, @, #) and the 1st/2nd/3rd digit give the 1st/2nd digits, the 3rd/4th digits, and the 5th/6th digits, respectively.
This translates a 7-figure number into a five-letter code word. It is essentially the same as Shirai's Graphical above. (Yatomi says there are various ways for checking and gives an example of using the 7th or 14th digit as a check digit.)
1. The number is divided into the 1st/2nd digits, the 3rd/4th digits, the 5th/6th digits, and the 7th digit.
2. The 1st/2nd digits, the 3rd/4th digits, and the 5th/6th digits are used to consult a Column Table consisting of four columns marked with symbols a (00-24), b (25-49), c (50-74), and d (75-99), which indicate a letter (A-Z; no Q; assignment is different from column to column) for the respective two digits 00-99. This results in three letters and a symbol sequence (aaa, aab, ..., ddd).
3. An Indicator Table has rows corresponding to the symbol sequences (aaa, aab, ..., ddd) and columns corresponding to 0-9 of the 7th digit. This gives two letters for the 7th digit.
4. The three letters from Step 2 and the two letters from Step 3 yield a five-letter code word.
For decoding, the five-letter code word is divided into the 1st to 3rd letters and the 4th and 5th letters.
1. The 4th and 5th letters give the 7th digit and the symbol sequence (aaa, aab, ..., ddd) by the Indicator Table.
2. The symbol (a, b, c, d) and the 1st/2nd/3rd digit give the 1st/2nd digits, the 3rd/4th digits, and the 5th/6th digits, respectively.
Sakai Kashichi (1939), Keiburu Kuraaku Tokuhon (Cable Clerk Reader) (Ditigal Library from the Meiji Era) proposes two schemes for 14-figure translation.
The first scheme (p.65), called 7 FIGURE CONDENSER, translates a 7-figure number into a five-letter code word. It is essentially the same as Shirai's Graphical above. (Sakai had published the X figure code above but must have judged Shirai's method better.)
1. The number is divided into the 1st digit, 2nd/3rd digits, the 4th/5th digits, and the 6th/7th digits.
2. The 2nd/3rd digits, the 4th/5th digits, and the 6th/7th digits are used to consult a Second Table, thus translating three numbers 00-99 into three letters and three Section Nos. (111, 112, ..., 444).
3. A First Table has rows corresponding to the Section Nos. (111-444) and columns corresponding to 0-9 of the 1st digit. This gives two letters (AA-YP) for the 1st digit.
4. The two letters from Step 3 and the three letters from Step 2 yield a five-letter code word.
For decoding, the five-letter code word is divided into the 1st and 2nd letters and the 3rd to 5th letters.
1. The 1st and 2nd letters give the 1st digit and the sequence of Section Nos. (111-444) by the First Table.
2. The Section No. (1-4) and the 3rd/4th/5th digit give the the 3rd/4th digits, the 5th/6th digits, and the 6th/7th digits, respectively.
Sakai's second scheme (p.66) claims to be capable of translating numbers 0-11,881,375 into five-letter code words. It is essentially a table for calculating base-26 representation.
The above procedure is often described with terms such as "figure code" and "condenser" but the usage of the terms depends on the author.
The broadest definition of "condenser" may be that by Rudolf-Mosse to refer to some means to represent numbers having more than five digits with a ten-letter code word. (A telegraphic word in cipher may contain up to five digits/letters, while a code "word" could contain up to ten letters.)
However, a condenser more often refers to means to represent two (or more) code words with one ten-letter code word. Friedman, "Report on the history of the use of codes and code language" (1928) p.23 follows this usage. The collocation "code condenser" would clearly indicate this meaning.
On the other hand, Abe Akira, Gaikoku Boeki Shoyo Ango Nyumon (1949) p.24 uses the term "condenser" to refer to a number translation table that may represent more than ten digits with a ten-letter code word. (Although he also mentions one that handle 10-figure numbers, he says it is not worth the name of "condenser.") Sakai uses the term to refer to a number translation table which results in less letters than the number of digits. This sense may be indicated by a collocation "figure condenser."
The term "figure code" may refer to either encoding with digits of a number, the translating numbers into code words, or the overall process encompassing both, though when one is used, the other seems to be always implied.
(The term "number translation table" used herein is a translation from Sakai's usage in Japanese, though Sakai himself uses the English word "converter" as an equivalent.)
British Books in Print for 1888 has a section "FIGURE CODES", which is advertised "In one word, an Order (or Offer) for any article, with Price, Quality, Shipment, and mode of Transit, can be transmitted." On the other hand, the actual codebooks listed appear to be ones for translating numbers into code words.
Bentley's essay on telegraphic code (Codes: Their Nature and Manipulation) uses "figure code" to refer to the overall process.
Acme p.900 has a sentence which uses the term "figure code" in three senses and yet manages to avoid being unclear.
Here, the "thirteen figure code" refers to the number translation table and the expression "private figure code" refers to an encoding tool. The next instance "figure codes" appears to be the overall process encompassing both.
For codebooks or references mentioned herein, see another article.