ネットワーク通信にしてもディスクなどの媒体への記録にしても,デジタルデータに多かれ少なかれエラーはつきもので,エラーが生じたときに検出・訂正ができるようにデータを構成する誤り検出符号や誤り訂正符号がいろいろ工夫されている.最も単純なものは,一組のデータ(数値)の和をデータに付しておくというチェックサムだろう.受信・読み取り時に和を計算して,データに付されているチェックサムと合わなければエラーがあったことがわかるというものである.エラーを検出するだけでなく,もとのデータを復元できる誤り訂正符号もある.
コンピューター時代以前の電信でも伝送ミスの問題はあり,さまざまな誤り防止方式が考案されていた.なかでも検誤表(mutilation table)と呼ばれるものはコード電報の誤り検出のみならず,訂正もできるという巧妙な仕組みだった.しかも,たった一枚の表でコードブックに収録された何万ものコード語のパターンをカバーできる(最大264=456,976パターン).
本稿では電信時代の誤り防止手段を概観した上で,その最も発展した形ともいうべき検誤表の仕組みについて解説する.
目次
電信のミスというのは日常茶飯事だが,普通の電文であれば一文字くらい間違っていても人間が見れば前後関係から正しいメッセージを読み取ることができる.だがそのような普通の文の冗長性が活用できないものとして,数字と電信コードがある.
数字の伝送の場合は一文字間違えば全く異なる数字になってしまい,致命的なミスにつながりかねないことは想像にかたくない.そこで,デジタルデータに使われるようなチェックサムの考えが提唱された.筆者の知る限り,電信でチェックサムの考えが初めて登場したのは1871年のことだった.綿花取引用のコードブックPrivate Telegraphic Code (1871)は複数の価格情報を(1/8単位の差分で)伝える数字のあとに各数字の和を付すことを提案している.改訂を重ねてロングセラーとなる同年のMeyerによるThe Cotton Telegraph Code (1871)は表によりチェック数字を定めてそれを付加する方式を提案していてチェックサムは使っていないが,Meyerが数年後に刊行した一般語彙用のThe General Telegraph Code (1874)ではコード語の各文字に対応する数字1〜26の和によるチェックサムを提案している.(以下,個々のコードブックについては別稿(英文)参照.)
ただし,Meyer (1874)は数字はそもそも伝送ミスが起こりやすいとして,チェックサムをコード語に直して送信することを提案している.このように,数字の送信ミスを防ぐために単語に直して送ることもこのころ一般的に行なわれるようになった.(当時のコードブックの多くは,伝送すべき平文の語句を表わすコード語として,数字や文字の羅列ではなく一般的な単語を使っていたが,各コード語に連番が付されていることが多かったので,それを利用して数字を単語に対応付けることができた.)単語であれば,先述のように一文字ミスがあっても人間が見れば訂正できる場合があるからである.
とはいえ,単語であっても一文字の違いで全く別の単語になってしまう例はいくらでもある.それはチェックサムを表わすものに限らず,コード語の送信一般に関わる問題なので,1870年ごろからコードブックを編集するときにスペルやモールス信号が似ているコード語を含まないようにするなどの配慮がされるようになっていった.
これはやがて,どの二つのコード語を取っても少なくとも2字は相違しているという「二字差」の概念につながった.1880年のアメリカのHartfieldによるThe Merchant's Code, extended and improvedと同年のイギリスのWhitelawの14,000 Latin Wordsはこの二字差の概念を謳っている.これにより,エラーによってコード語が別のコード語に変わってしまう可能性は大きく低下するので,1870年代に登場したチェックサムは次第に使われなくなっていく.(1930年代に二字差を使えない三字コードが登場すると再び脚光を浴びるようになる.)
エラーの訂正はエラーの検出とはまた別の問題である.二字差により,一文字のエラーがあった場合には該当するコード語がみつからないので誤りがあったことは確実に検出できるのだが,誤りがコード語の先頭付近で発生すると本来のコード語を特定することは難しい.そこで考え出されたのが語尾索引(terminational order, terminal indexなどという)である.これはコードブックに収録されている全コード語を末尾からのアルファベット順に配列したもので,受信されたコード語の後半が正しい場合に本来のコード語をみつけ出すのに使うことができる.これを最初に採用したのはWhitelawが出版者となっている25,000 English Words (1879)と思われる.

上記25,000 English WordsはTelegraph Detectorと称して電信符号上誤りやすい文字の一覧も掲載している.多くのコードブックに掲載されているこのような表を参照することにより,送信エラーがみつかったときに,本来の文字をみつける助けになる.

語尾索引が登場した時期はまだコード語は英仏独語等の8か国語のいずれかの単語でなければならないという規定があったのだが,1903年の国際電信規則の改定により発音可能であれば人工語でもよいことになった(別稿(英文)参照).その一方,コード語の字数は10字までとされていた.このため,あらゆるコード語を5字で構成し,2つのコード語をつなげて10字のコード語とすることで,電文の語数,ひいては電信料金を半分にできるコードブックが広まった.このような5字コードの登場が,機械的にコード語を構成し,エラーの検出・訂正まで可能にする検誤表に道を開くことになった.
検誤表の具体例は下記でいくつか紹介するが,ここではまず,アルファベットの文字数を7字に減らしたバージョンでその仕組みを説明する.

このように,検誤表は左上・左下・右下の3セクションからなり(左上・右上・右下のこともある),この左上セクションが5字コードの最初の2字を,左下セクションが第3字を,右下セクションが最後の2字を表わしている.コードブックに含まれるコード語はすべてこの表に従って作られている(このためmutilation tableではなくconstruction tableと呼ぶこともある).
このような検誤表があれば,最初の2字と最後の2字が与えられたとすると,左上セクションで最初の2字を見つけ,そこから下にたどっていき,右下セクションで最後の2字を見つけ,そこから左にたどっていき,両者が左下セクションで交わったところにある文字が第3字となる.この関係を使うことによって,5字コードのうち4字が与えられれば,残りの1字を特定することができるのである.(もちろん,5字コードのうちどの1字が間違っているかはわからないので,それに応じて5通りの候補がみつかることになるが,文脈から絞り込むことができる.また,表のあらゆる組み合わせが実際にコード語として使われているわけではないので候補が5通りも存在しないこともある.)
このように,5字コードのうちの4字が決まれば残りの1字も決まるということは,この表に従って構築されるコード語が「二字差」の条件を満たしていることを意味する.仮に満たしていないとすると(つまり,1字のみしか違わない2つのコード語があったとすると),4字が決まっても残りの文字に2通りの可能性があることになる.
検誤表が考案されるまでは,5字コードの作成者は2字差を実践しようとすれば,注意して1字違いのコード語を排除していく必要があった.だが,このような表に基づいてコード語を構築することにより,自動的に二字差の条件が満たされることが保証される.
コード編纂者は,5字コードが二字差を満たしていることを語尾索引を使って検証するような作業をしていくうちに,最初からこのような表に従ってコードを作成することを思いついたのだろう.検誤表はユーザーのみならず,コードブックの編纂者にとっても強力なツールなのである.
さらに,この表をうまく作れば,単に1字違いのコード語を排除する(「二字差」)のみならず,隣り合う文字を入れ替わったコード語も排除することができる.そうすれば,たとえばAMNEDがコード語だったとすると,MとNが入れ替わったANMEDはコード語として採用されず,そのような入れ替わりがあってもエラーだと検出できるようになる.
上記の縮小バージョンの検誤表で,第1字と第2字が入れ替わってしまったコード語が存在しないという条件は,(第3字は変わらないので)入れ替わったパターンが同じ縦列上にないという条件と等価になる.この条件は,上記のような規則的なパターンの場合,左上の表の縦のます目の数(つまりアルファベットの文字数)が奇数であれば満たされることがわかる(偶数だったら,1字目と2字目の間隔が文字数の半分になるところ(例:AとDの間隔は6の半分の3)で,下図(左)の赤の部分のように入れ替わったパターンが同じ縦列上に繰り返し現われてしまう).
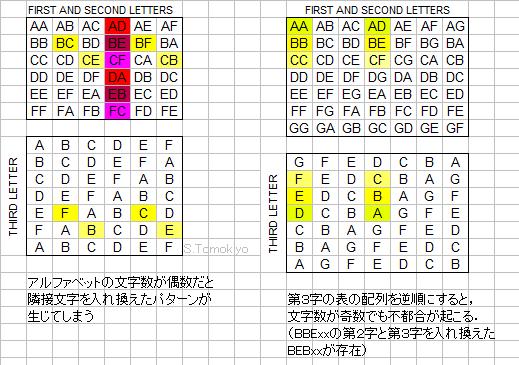
第2字と第3字の入れ替わったコード語が存在しないという条件はもう少し難しい.BCのCが第3字のFと入れ替わる場合を考えると,入れ替わり後のBFの縦列上で,かつもとの第3字であるFの横列上(第4〜5字は変わらないので)の交点の位置にCがこなければよい.図形的に考えると,左上の表のBCとBFの対に対して,左下の表でFとCの対がその真下にこなければよい.このようなパターンが生じるのは,CからFに進む数とFからアルファベットの終点を経て巡回的にCに進む数が等しくなる場合(入れ替わる第2字と第3字の間隔が文字数の半分の場合)であり,文字数が偶数だと上図(左)の黄色の部分のようにこのようなパターンが生じてしまう(BCFxxとそのCとFを入れ替えたBFCxxが両方ともコードに存在).一方,文字数が奇数であればそのようなパターンが避けられる.
ただし,上図(右)のように,左下の表(第3字の表)の配列を逆順にすると,文字数が奇数でも問題が生じてしまう.(アルファベットの終点を経る必要がないので,アルファベットの文字数が関係なくなる.)下記のSchofieldの検誤表がこのパターンに該当する.
現実にはアルファベットには26文字があり,単純に検誤表を作成すると文字数が偶数なので,互換エラー防止の観点からは不都合をきたすことになる.その対策として,1920年代以降のコードブックではいろいろな工夫がこらされるようになる.
最も単純なのはアルファベットのうちたとえばQを使わないことにして文字数を25と奇数にする方式である.
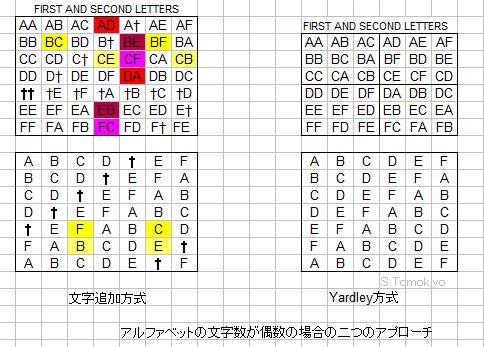
それとは逆に,Kahn, The Codebreakers p.848ではアルファベットにたとえば記号「†」を追加することによって文字数を奇数にする方式を紹介している.そのような表からできるパターンのうち,「†」を含むものを使わないことにすれば,アルファベット26文字を最大限に利用しつつ,隣接文字互換の対策もできる検誤表が作成できる.下図(左)の赤・黄色部分を見れば,上記で問題になったパターンがずれるようになっているのがわかる.
後述するYardleyらではアルファベット26文字を13文字ずつに分けて表を構成することで,各セクションの文字数は奇数にしている.イメージとしては下記の右図のような具合になる.
筆者の知る限り最初の検誤表は神戸のスコフィールドによるSchofield's Eclectic Phrase Code (1914)の"Analysis for Tracing Mutilations"である.筆者が見たのは1925年の「6th reprint: printed by photo-zyncotype process from the original 1914 edition」(Introductionの日付はDecember 1914)でしかないが,この表示を特に疑う理由はない.この表示がある扉ページには「International Copyright Secured 1919. United States Copyright Secured 1920.」との表示もあるが,後者については下記のとおりCatalog of Copyright Entries for the Year 1920(Google)で確認できた.(ちなみに,所蔵大学図書館のOPACで刊行年が"c1920"と表示されるのはこれを典拠にしたものだろう.)

ただし,Schofieldは特にこの検誤表を画期的なものであるかのような書き方はしていない.コード編纂者の間ではいつのまにか当たり前になっていたのかもしれない.(ユーザー向けに検誤表として掲載されていないコードブックであっても,作成にはこうした表を使っていた可能性はある.収録されている全コード語を電子データ化して調べればコード語の選定がそのような原則に従っているかどうかは検証できるだろう.)コードブックに採用される前に研究者が提案した論文があったことも考えられる.
Schofieldの検誤表が初期のものである傍証として,上記でも触れたように,隣接文字の入れ替わり対策をしていないことが挙げられる.たとえばOCOxxというコード語に対して第2・3字が入れ替わったOOCxxというコード語が存在している.文字Qを省いているのは,アルファベットの文字数を奇数にするための工夫ではなく,おそらく下記の「発音可能要件」のためだろう.(Qは次にU+母音がこなければならないのでコードに採用しても作成できるコード語の数に限りがあり意味がないと考えたのだろう.)
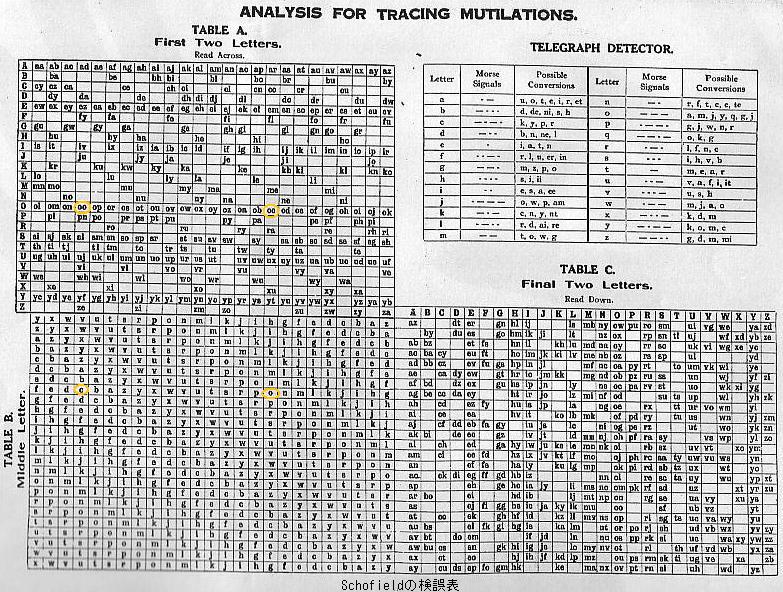
上記の検誤表では,随所に空白がある.これは1928年まではコード語が発音可能であることが国際電信規則で必須と規定されていたため,発音できない(と電信局で判断されるおそれのある)文字のつながりを避けたためと思われる.(ただし,別稿(英文)で説明するように,「発音可能」という条件は徐々に拡大解釈されていき,コード編纂者は次第に大胆になっていった.)下記で挙げるコードブックでも,発音可能であることが必須でなくなった1930年代以降のものにはそのような空欄はない.
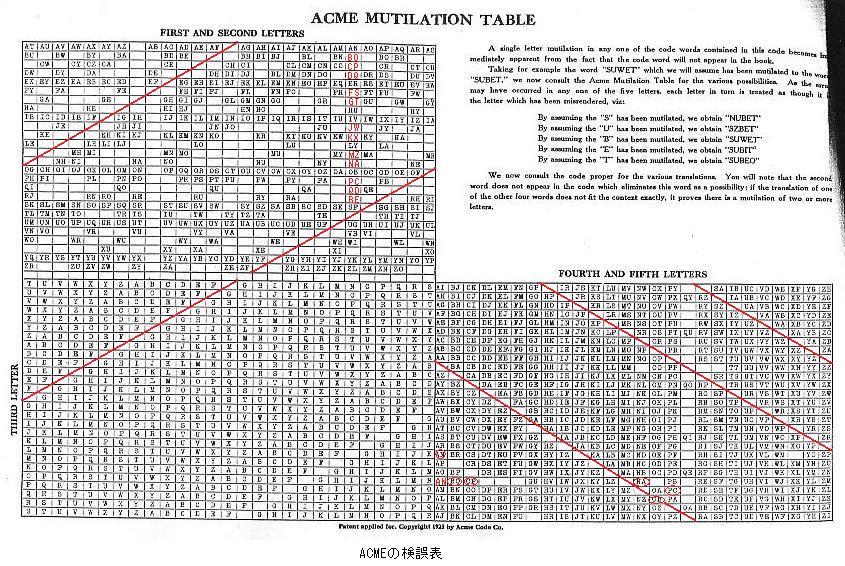
1920年に刊行されたABC Codeの第6版がまだ検誤表でなく語尾索引を使っていたように,1920年の時点では検誤表をコードブックに掲載するのは一般的とはなっていなかった.普及のきっかけはYardleyらによるUniversal Trade Code (1921)とA. C. Meisenbach ("Acme")によるAcme Commodity and Phrase Code (1923),特に広く使われた後者であるように思われる.(阿部『外国貿易商用暗号入門』p.10)は伝聞と断った上でUniversalが最初と述べているが,Schofieldは1914年,米国での著作権登録でも1920年でこれより早い.さらに,米国陸軍省の1915年の電報コードも検誤表を採用していた(別稿(英文)参照).)
YardleyらもACMEも検誤表そのものを画期的なものだとは述べていない.Yardleyらは単にメッセージに誤りがあっても検誤表を使って復元できると簡単に述べるに留まっている.
ACMEの前付け解説では「他の検誤表」と比べればAcme Mutilation Tableの優秀さがわかるといった記述をしていることから,ACMEが検誤表そのものを創始したことまでは主張していないことは明らかだ.ただし,ACMEが新規としているのは,文字がアルファベット順になっていて簡単で使いやすいという点であり,たとえば下記中山(1938)のようなものが当時主流であったのであればそれもうなずける.だが,YardleyらやSchofieldのものと比べるとこの点で新味があるとは思えない.ACMEはこの検誤表で特許を出願した旨を記しているが,登録されたのだろうか.(Google Patentで検索する限り見当たらない.)
Yardley (1921)とAcme (1923)はいずれも隣接文字を入れ替えたコードが存在しないことを謳っている.そのためには上記のようにアルファベットの文字数を奇数にするなどの工夫が必要になるが,両者はそれぞれ独自の方式を使っている.
Yardleyらの"Mutilation Table"では,2文字パターンを表わす表(左上と右下)を13×13の4セクションに区分することで,各セクションの文字数が奇数になるようにしている.
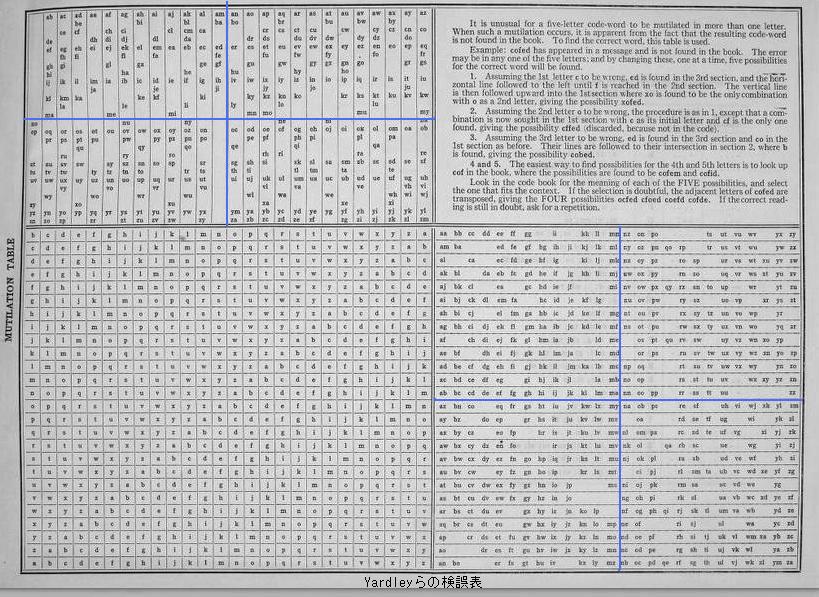
"Acme Mutilation Table"は一見,アルファベットのFとGの間に一文字を追加する,Kahnが紹介したような方式で「†」を含む欄を空欄としたもののように見えるが,もう少し込み入っている.たとえば左上の表でANの列の空欄を埋めてみると,ANに対するNA,OBに対するBOなどの互換パターンが同じ列中に存在している.よく見ると,左上の表の列数は空欄を含め27になっているが,行数は26と偶数のままなのである.
右下の表では左端の列のANに相当する欄が空欄になっているが,同じ行のNAとの互換パターンを避けるために3つ上の欄に移されたものと思われる.一方,同じ行ではBOやCPの互換パターンのOBやPCも生じるはずだが,O, Pの列を見てみるとOB, PCはやはりそれぞれアルファベット順を外れて少し下の行に移されている.
このように,ACMEの検誤表は,第2字と第3字の互換パターンを避けるために左上の表の列数,右下の表の行数が奇数になるよう空欄を加えつつ,第1字と第2字,第4字と第5字の互換パターンを避けるためには個別に空欄を設けたり位置をずらしたりして対応している.
三菱『和文電信暗号』の検誤表(「羅馬字暗号原表」)は1928年に採択された新たな電信規則に対応したもので,2つの5字コードをつなげるとCategory Aとして規定された10字までの電信語の要件(別稿(英文)参照)を満たすように構成されている.Category Aの定義は込み入っているが,5字,10字については次のようなものである.
2つつなげて上記の定義に合う10字コードを作れるようにするには,5字コードが二つの母音を含むようにすればよい(10字のうち母音は3つでよいので,若干無駄ではあるが,どれとどれがつなげて使われるかはわからないのでやむを得ない).
簡単にいうと,次のような4枚の検誤表がある(V=母音,C=子音,X=どちらでもよい).
甲表(イ):VC-V-XXまたはCV-V-XX(後者の場合,語尾部のパターンXX=VCは不使用)
甲表(ロ):VC-C-VCまたはVC-C-CVまたはCV-C-VCまたはCV-C-CV(VC-C-CVの場合,追加条件あり)
乙表:VV-C-XX
丙表:CC-V-XX
凡例は,丙表の語が二つ続くと「母音が三つ」という要件を満たさなくなるのでその場合は1語につなげずに別々に送信する必要があるが,「極めて僅少」なパターンであると説明している.

2文字の交換防止までは考慮されておらず,nydat/nydtaやovzxe/owzex(いずれも暗号原表の甲表(ロ))のような例がある.
なお,ややこしカテゴリーAは1932年の電信規則改正で廃止され,以後は語長は5字までに制限された代わりに母音がどうのという制限はいっさいなくなった.
New Boe Code (1937) の"Table for Correction of Mutilated Codewords"(BellovinのFig. 6参照)はQを省くことで25文字としている.
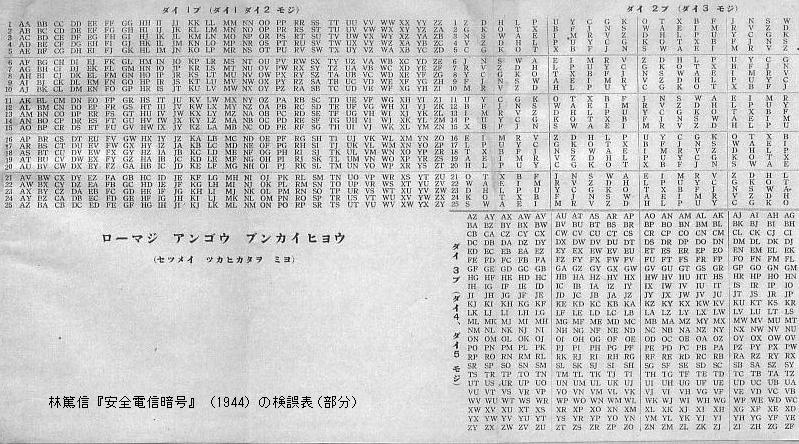
林篤信『安全電信暗号』(1944)の「ローマ字暗号分解表」もこれに近いが,右上の表の各列内の文字の配列がランダムになっている.「転置防ぎとて,となりあった文字またはひとつおきの文字をおきかえてもほかの暗号と同じにならぬようにされたところの最新式の暗号である」ということなので,隣接文字のみならず一つ置きの文字の互換も防ぐためらしい(未検証).
Bentley's Second (1929)の"Mutilation Table"もこれに近いが,第2・3・5字の配列がランダムになっている.このコードブックのコードも隣接文字のみならず一つ置きの文字の互換,さらにはモールスによる送信の空白の取り方によるエラー[ER ". ._."とUE ".._ ."の取り違えの類だろう]も検出できるとしている.
一方,ABC Code (7版) (1936) の"Key to Codewords"は左上・右上・右下のセクションをもつ25文字アルファベットだが,左上の表は25行26列と列が1つ多くなっている.また,第1・4・5字はアルファベット順だが,第2字の配列が不規則になっている.第3字はアルファベット順ではないが規則的.
中山久美『和欧商事電報暗号』(1938)の「検誤表」は26×26という偶数文字の表だが,その代わり文字の配列の規則性を乱すことによって文字の入れ替えを防ごうとしている模様(未検証).


上記では世界標準であった英字5字コード用の検誤表を紹介したが,日本では1940年代になるとカナの和文用コードにも検誤表を導入するものが出てきた.(以下,個々の和文コードブックについては別稿参照.)
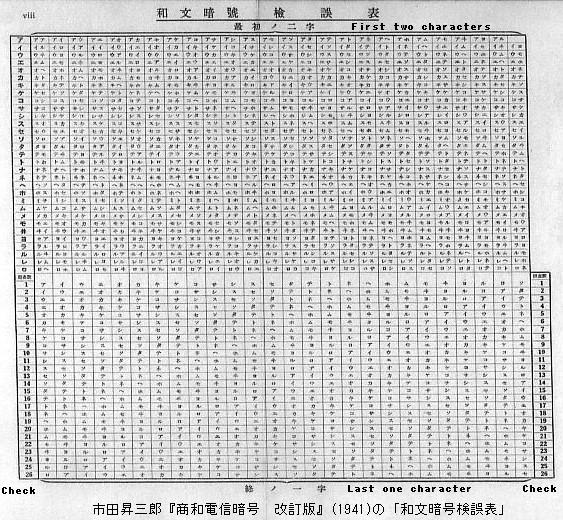
市田昇三郎『商和電信暗号 改訂版』(1941)では各コード語に「照査数」という1〜26の番号が割り当てられており,これを誤り検査に使えるようになっている.3つのコード語の照査数を合計した数字(3〜78)を表により文字(数字または「ク」「チ」「ツ」などコード語に使われていない所定のカナ)に変換し,それを「照査(チェック)字」として付けて送信する.受信側では照査字から照査数を復元して「和文暗号検誤表」を使って誤り検査をする.
この検誤表は,カナ3字のコード語のうち最初の2字と照査数を指定すると第3字が特定できるようになっている.これを応用してカナ3字のコードのうちの2字がわかれば残りの1字を特定できる.なお,照査数の復元について,送られてくるのは3つのコード語の照査数の合計だけであるが,3つのうち2つのコード語が正しければ,それらの照査数と送られてきた和(チェックサム)の差から誤っているコード語の照査数を復元できる.
なお,このコードブックには英字3字コードも併記されており,同様の「欧文暗号検誤表」がある.また,やはり英字3字コードを採用した中山久美『日本通商暗号』(1950)も同様の「欧文電報検誤表」を掲げている.(このような方式の英字3字コード用の検誤表は森岡久雄のParamount Simple-check Three Letter Code (1934)に掲載されており,同書はこれがこれまで考案されたものとは全く異なると述べている.)
中山久美『商事電報略号 : 自査式二字制』(1952)は2字コードで,コード語の第1字,第2字をそれぞれ横軸,縦軸にとってあらゆる組み合わせを示した「自査式二字制 商事電報略号検誤表」を掲載している.その各行に「査数」(チェック数字)を割り当てていて,コード本体では各コード語にその査数が付記されている.用法は3字コードの市田(1938)や中山(1950)と同様で,コード語3つごとに査数の和に応じた「検字」を送ることになっており,受信側では査数を手がかりに検誤表を使って誤りを訂正する.
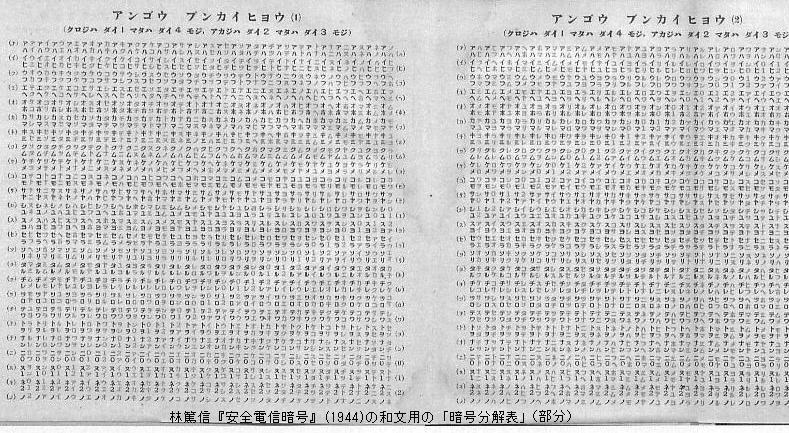
上記で紹介した林篤信『安全電信暗号』(1944)はカナ用の「暗号分解表」も掲載している.和文コードはカナ4文字からなるが,暗号分解表は第1/4文字(黒字)と第2/3文字(赤字)の可能な組み合わせを挙げている.基本的には縦軸にインターリブ式にア〜ン,0,1,2(本書では0,1,2がコードを構成するカナ文字に追加されている)が割り当てられ(黒字),横軸には順次ずらしながらア〜ン,0,1,2が割り当てられ(赤字),各ますにはカナ2文字(黒字+赤字)がはいる.4字コードの前半と後半は同じ縦列に属するものという制限が課してあるので,4字のうちの3字がわかれば,前半か後半かどちらかの2文字は特定できる.
松本光晴『和文電略暗號帳』(1939)の「誤電点検表」は誤り検査だけでなくコードの曖昧さ解消も兼ねている.このコードブックは基本的にはカナ2字コードだが,濁点・半濁点や「ン之部」のコードで識別される第二部門・第三部門・第四部門・第五部門もある.濁点・半濁点を使わずに「引合符号」によって部門を区別することもできるようになっているのだが,この引合符号を誤り検査にも使っているのである.